Affine Point Processes: Approximation and Efficient Simulation

Abstract

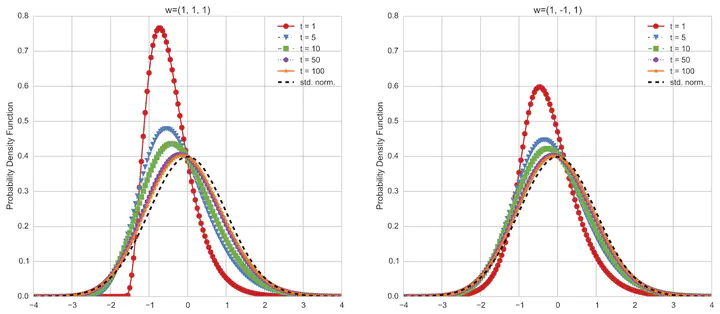
We establish a central limit theorem and a large deviations principle for affine point processes, which are stochastic models of correlated event timing widely used in finance and economics. These limit results generate closed-form approximations to the distribution of an affine point process. They also facilitate the construction of an asymptotically optimal importance sampling estimator of tail probabilities. Numerical tests illustrate our results.