Sparse Additive Contextual Bandits: A Nonparametric Approach for Online Decision-making with High-dimensional Covariates

Abstract

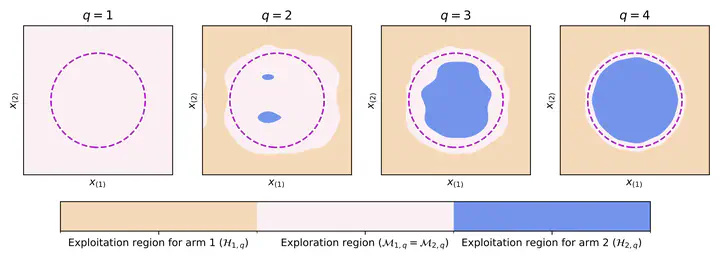
Personalized services are central to today’s digital landscape, where online decision-making is commonly formulated as contextual bandit problems. Two key challenges emerge in modern applications: high-dimensional covariates and the need for nonparametric models to capture complex reward-covariate relationships. We address these challenges by developing a contextual bandit algorithm based on sparse additive reward models in reproducing kernel Hilbert spaces. We establish statistical properties of the doubly penalized method applied to random regions, introducing novel analyses under bandit feedback. Our algorithm achieves sublinear cumulative regret over the time horizon $T$ while scaling logarithmically with covariate dimensionality $d$. Notably, we provide the first regret upper bound with logarithmic growth in $d$ for nonparametric contextual bandits with high-dimensional covariates. We also establish a lower bound, with the gap to the upper bound vanishing as smoothness increases. Extensive numerical experiments demonstrate our algorithm’s superior performance in high-dimensional settings compared to existing approaches.