Staffing under Taylor's Law: A Unifying Framework for Bridging Square-root and Linear Safety Rules

Abstract

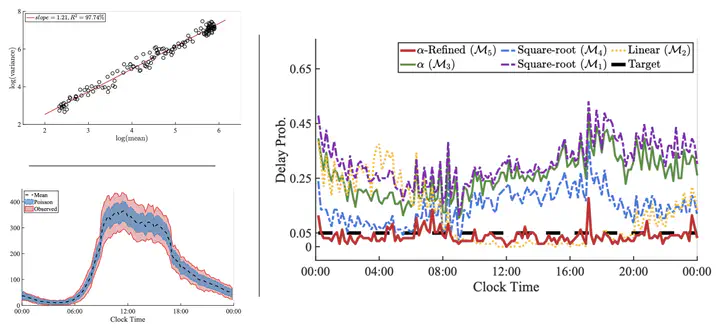
Staffing rules serve as an essential management tool in service industries to attain target service levels. Traditionally, the square-root safety rule, based on the Poisson arrival assumption, has been commonly used. However, empirical findings suggest that arrival processes often exhibit an `over-dispersion’ phenomenon, in which the variance of the arrival exceeds the mean. In this paper, we develop a new doubly stochastic Poisson process model to capture a significant dispersion scaling law, known as Taylor’s law, showing that the variance is a power function of the mean. We further examine how over-dispersion affects staffing, providing a closed-form staffing formula to ensure a desired service level. Interestingly, the additional staffing level beyond the nominal load is a power function of the nominal load, with the power exponent lying between 1/2 (the square-root safety rule) and 1 (the linear safety rule), depending on the degree of over-dispersion. Simulation studies and a large-scale call center case study indicate that our staffing rule outperforms classical alternatives.