''Over-optimizing'' for Normality: Budget-constrained Uncertainty Quantification for Contextual Decision-making

Abstract

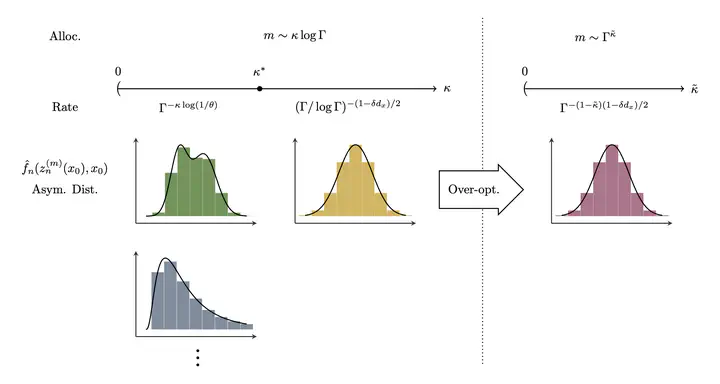
We study uncertainty quantification for contextual stochastic optimization, focusing on weighted sample average approximation (wSAA), which uses machine-learned relevance weights based on covariates. Although wSAA is widely used for contextual decisions, its uncertainty quantification remains limited. In addition, computational budgets tie sample size to optimization accuracy, creating a coupling that standard analyses often ignore. We establish central limit theorems for wSAA and construct asymptotic-normality-based confidence intervals for optimal conditional expected costs. We analyze the statistical–computational tradeoff under a computational budget, characterizing how to allocate resources between sample size and optimization iterations to balance statistical and optimization errors. These allocation rules depend on structural parameters of the objective; misspecifying them can break the asymptotic optimality of the wSAA estimator. We show that ‘‘over-optimizing’’ (running more iterations than the nominal rule) mitigates this misspecification and preserves asymptotic normality, at the expense of a slight slowdown in the convergence rate of the budget-constrained estimator. The common intuition that ‘‘more data is better’’ can fail under computational constraints: increasing the sample size may worsen statistical inference by forcing fewer algorithm iterations and larger optimization error. Our framework provides a principled way to quantify uncertainty for contextual decision-making under computational constraints. It offers practical guidance on allocating limited resources between data acquisition and optimization effort, clarifying when to prioritize additional optimization iterations over more data to ensure valid confidence intervals for conditional performance.