Affine Point Processes: Approximation and Efficient Simulation
Abstract
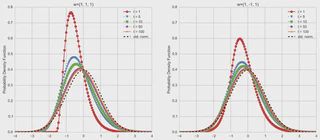
We establish a central limit theorem and a large deviations principle for affine point processes, which are stochastic models of correlated event timing widely used in finance and economics. These limit results generate closed-form approximations to the distribution of an affine point process. They also facilitate the construction of an asymptotically optimal importance sampling estimator of tail probabilities. Numerical tests illustrate our results.
Type
Publication
Mathematics of Operations Research 40(4):797–819
Affine Point Process
Affine Jump-Diffusion
Large Deviations
Importance Sampling
Rare Event Simulation

Authors
I am an Associate Professor at HKUST, jointly appointed in the Department of Industrial Engineering and Decision Analytics and the Department of Economics, and the Academic Director of the MSc in FinTech program. I serve as an Associate Editor for several leading journals in the field, including Management Science, Operations Research, Navel Research Logistics, and Queueing Systems.

Authors
Professor in the Department of Management Science and Engineering, Stanford University.

Authors
Professor in the Department of Management Science and Engineering and Director of the Mathematical and Computational Finance Program at Stanford University.

Authors
Thomas W. Ford Professor in the Department of Management Science and Engineering, Stanford University.