High-Dimensional Simulation Optimization via Brownian Fields and Sparse Grids

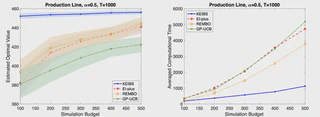
High-dimensional simulation optimization is notoriously challenging. We propose a new sampling algorithm that converges to a global optimal solution and suffers minimally from the curse of dimensionality. The algorithm consists of two stages. First, we take samples following a sparse grid experimental design and approximate the response surface via kernel ridge regression with a Brownian field kernel. Second, we follow the expected improvement strategy—with critical modifications that boost the algorithm’s sample efficiency—to iteratively sample from the next level of the sparse grid. Under mild conditions on the smoothness of the response surface and the simulation noise, we establish upper bounds on the convergence rate for both noise-free and noisy simulation samples. These upper bounds deteriorate only slightly in the dimension of the feasible set, and they can be improved if the objective function is known to be of a higher-order smoothness. Extensive numerical experiments demonstrate that the proposed algorithm dramatically outperforms typical alternatives in practice.