Smooth Nested Simulation: Bridging Cubic and Square Root Convergence Rates in High Dimensions

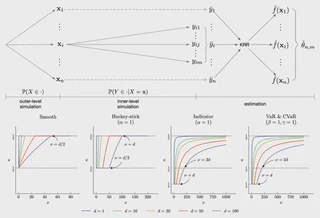
Nested simulation concerns estimating functionals of a conditional expectation via simulation. In this paper, we propose a new method based on kernel ridge regression to exploit the smoothness of the conditional expectation as a function of the multidimensional conditioning variable. Asymptotic analysis shows that the proposed method can effectively alleviate the curse of dimensionality on the convergence rate as the simulation budget increases, provided that the conditional expectation is sufficiently smooth. The smoothness bridges the gap between the cubic root convergence rate (that is, the optimal rate for the standard nested simulation) and the square root convergence rate (that is, the canonical rate for the standard Monte Carlo simulation). We demonstrate the performance of the proposed method via numerical examples from portfolio risk management and input uncertainty quantification.

Management Science 70(12):9031-9057